来源：晓飞的算法工程笔记 公众号，转载请注明出处

论文: Training-Free Model Merging for Multi-target Domain Adaptation

• 论文地址：https://arxiv.org/abs/2407.13771
• 论文代码：https://air-discover.github.io/ModelMerging

创新点

• 对域适应的场景解析模型中的模式连通性进行了系统的探索，揭示了模型合并有效的潜在条件。
• 引入了一种模型合并技术，包括参数合并和缓冲区合并，适用于多目标域适应任务，可应用于任何单目标域适应模型。
• 在数据可用性受限的情况下，也能达到与使用多个合并数据集进行训练相当的性能。

内容概述

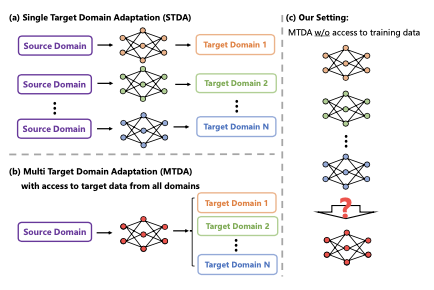
论文研究的是场景理解模型的多目标域适应（MTDA）。虽然之前的方法通过领域间一致性损失取得了可观的结果，但它们通常假设可以不切实际地同时访问所有目标领域的图像，忽略了数据传输带宽限制和数据隐私等问题。鉴于这些挑战，论文提出了一个问题：如何在不直接访问训练数据的情况下合并在不同领域独立适应的模型？

对此问题的解决方案包含两个部分，即合并模型参数和合并模型缓冲区（即归一化层统计数据）。在合并模型参数方面，模式连通性的实证分析意外地表明，对于使用相同的预训练主干权重训练的单独模型，线性合并就足够了。在合并模型缓冲区方面，使用高斯先验来建模现实世界分布，并从单独训练模型的缓冲区中估计新的统计数据。

论文的方法简单而有效，取得了与数据组合训练基线相当的性能，同时消除了访问训练数据的必要性。

方法

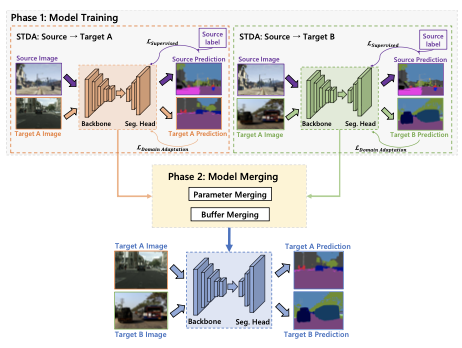
以往的方法假设，在适应阶段能够同时访问所有目标领域图像的非实际假设。相反，论文方法的流程包括两个不同的阶段：

1. 单目标域适应阶段，分别训练适应于各个目标领域的模型。简单地采用最先进的无监督域适应方法HRDA，利用各种主干架构，如ResNet和视觉Transformer。
2. 模型合并阶段（主要关注点），专注于将这些适应后的模型合并在一起以创建一个稳健的模型，而不需要访问任何训练数据。该方法包含模型的两个关键组成部分：参数（即可学习层的权重和偏置）和缓冲区（即归一化层的运行统计信息）。

参数合并

论文通过对比实验发现，当从相同的预训练权重开始时，域适应模型能够有效地过渡到多样的目标领域，同时在参数空间中保持线性模式连接。因此，这些训练模型之间的简单中点合并可以生成在两个领域中都具有鲁棒性的模型。

缓冲区合并

缓冲区，即用于批归一化（BN）层的运行均值和方差，与领域有密切关系，因为它们封装了特定领域的特征。现有方法主要处理在同一领域内对两个训练于不同子集的模型的合并，而论文研究在完全不同目标领域中训练的两个模型的合并，因此缓冲区合并的问题变得不再简单。

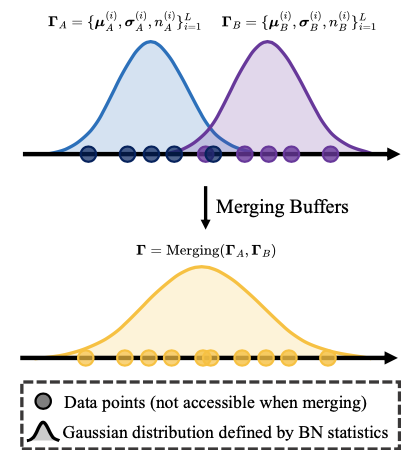
BN层的引入是为了缓解内部协变量偏移的问题，即输入的均值和方差在经过内部可学习层时发生变化。在这种背景下，基本考虑是后续的可学习层预期合并的BN层的输出遵循正态分布。由于输出的BN层保留了输入符合高斯先验的归纳偏见，因此可以从 \(\mathbf{\Gamma}_A\) 和 \(\mathbf{\Gamma}_B\) 中获取的值来估计 \(\boldsymbol{\mu}^{(i)}\) 和 \([\boldsymbol{\sigma}^{(i)}]^2\) 。首先获得来自该高斯先验的数据点的均值和方差的两个集合，以及这些集合的大小，共同利用这些值来估计该分布的参数。

当将合并方法扩展到 \(m (m \geq 2)\) 个高斯分布时，可以按如下方式计算已跟踪批次的数量 \(n^{(i)}\) 、均值的加权平均 \(\boldsymbol{\mu}^{(i)}\) 和方差的加权平均。

主要实验

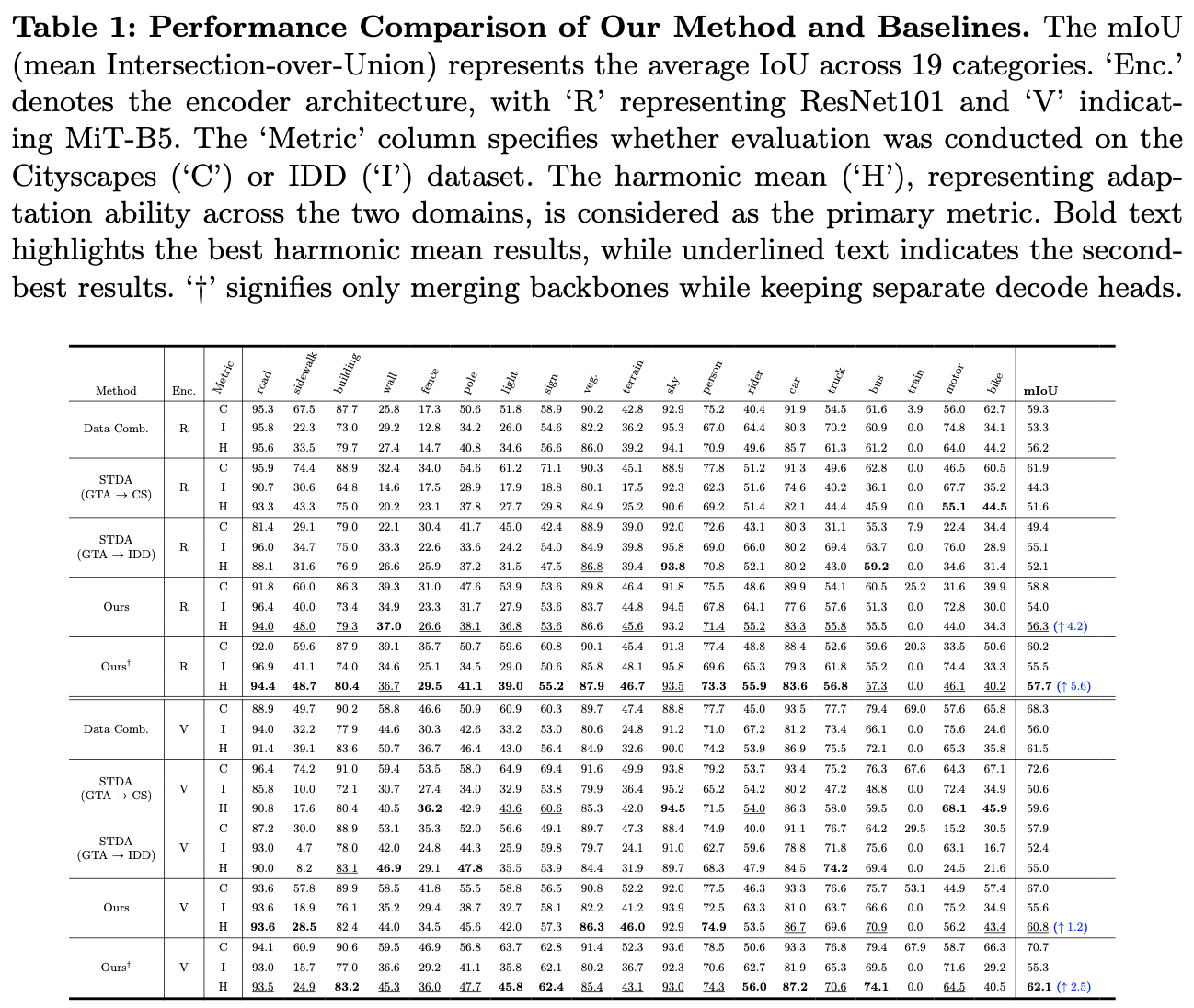
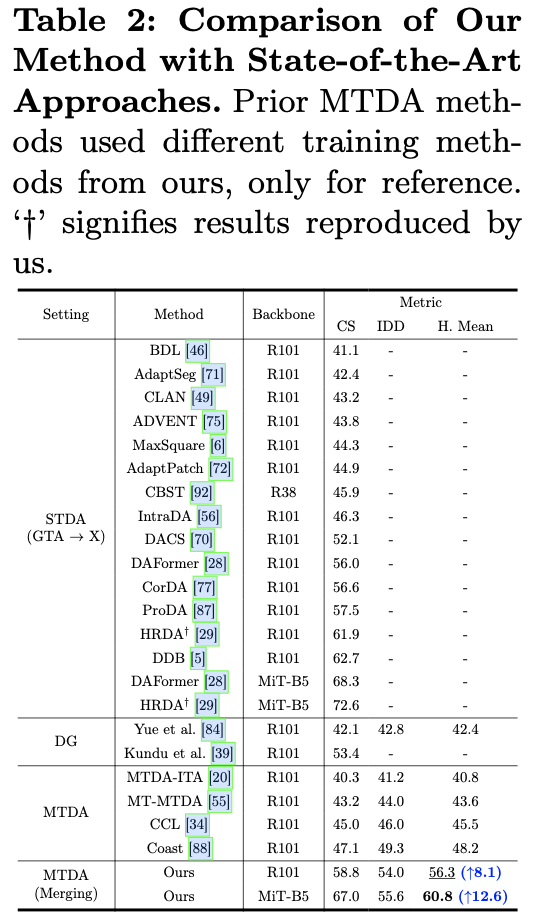
如果本文对你有帮助，麻烦点个赞或在看呗～
更多内容请关注 微信公众号【晓飞的算法工程笔记】